what is the resultant moment about a due to the distributed load? (figure 1)
Beam Analysis – Shearing force
Beam Analysis – For equilibrium in a beam the forces to the left of any section such as X as shown in Fig. 1(a) must remainder the forces to the correct of the department X. Too the moments nigh Ten of the forces to the left must balance the moments almost 10 of the forces to the correct.
Although, for equilibrium, the forces and moments cancel each other, the magnitude and nature of these forces and moments are important as they determine both the stresses at 10, and the beam curvature and deflection. The resultant force to the left of X and the resultant force to the right of X (forces or components of forces transverse to the axle) establish a pair of forces tending to shear the beam at this section. The shearing force is defined as the force transverse to the axle at any given section disposed to crusade it to shear at that section.
Past convention, if the tendency is to shear as shown in Fig. one(b), the shearing forcefulness is regarded as positive (i.e. +F); if the tendency to shear is equally shown in Fig. 1(c), it is regarded every bit negative (i.east. –F).
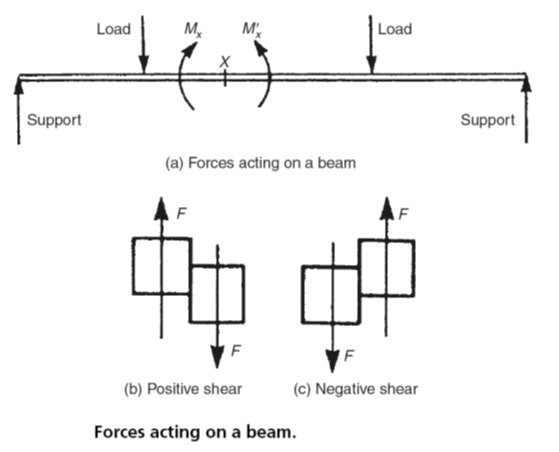
Fig. i
Bending moment
The bending moment at a given section of a beam is divers as the resultant moment about that section of either all the forces to the left of the section or of all the forces to the right of the section. In Fig. one(a) the angle moment is either Thoux or Chiliad'x . These moments will exist clockwise to the left of the department and anticlockwise to the right of the section. They will crusade the beam to sag. By convention this sagging is regarded as positive bending. That is, positive bending moments produce positive bending (sagging). Similarly negative angle moments cause the beam to curve in the opposite direction. That is, negative bending moments produce negative bending (hogging). The difference between sagging and hogging is shown in Fig. ii.
Contraflexure is present when both hogging and sagging occurs in the same beam as shown in Fig. two(c). For the loading shown in Fig. 2(a), the beam volition sag between the points B and C, and for the loading shown in Fig. 2(b) the beam will hog between the points A and B.
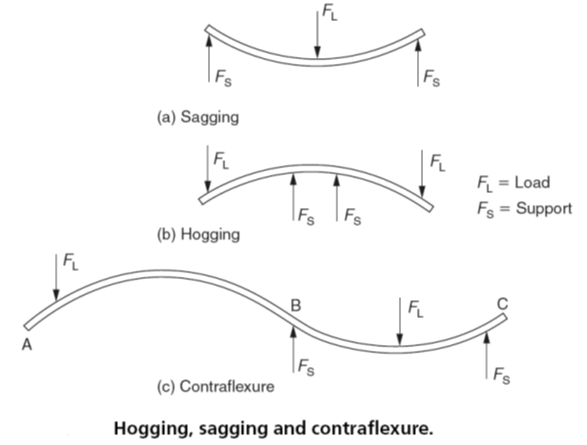
Fig. 2
The values of shearing force and angle moment will usually vary forth whatever beam. Diagrams showing the shearing forces and the angle moments for all sections of a axle are called shearing force diagrams and angle moment diagrams, respectively.
Shearing forces and shearing strength diagrams are less important than bending moments and bending moment diagrams; however, they are useful in giving pointers to the more important aspects of a bending moment diagram. For case, wherever the shearing force is zero, the angle moment volition exist at a maximum or a minimum.
Shearing force and bending moment diagrams
Consider the shearing forcefulness and bending moment diagrams for the system of forces acting on the beam in Fig. iii. For the moment, only a elementary system of three point loads will exist considered.

Fig 3
Information technology is first necessary to summate the reactions at A and B as previously described in Department. The axle is simply supported at A and B. This means that it rests on supports at these points giving vertical reactions. The general weather condition for equilibrium crave that the resultant moment about any point must exist nix, and the sum of the upward forces must equal the sum of the downward forces. Therefore, taking moments about A, the moment for R B must residuum the moment for the load C:
R B ×8m =24 kN ×5m
R B =(24 kN ×five thou)/8m
R B =xv kN
Similarly:
R A =24 kN -15 kN =9kN
Immediately to the right of A the shearing strength is due to R A and is therefore 9 kN. Every bit this force is to the left of the department considered it is upwards, hence the shearing force is positive. The shearing force volition exist abiding for all points between A and C as no other forces are practical to the beam between these points.
When a betoken to the right of C is considered, the load at C every bit well as the reaction strength R B must be taken into account. Alternatively R B on its own can be considered. The shearing force will exist fifteen kN. This is the value previously calculated for R B or it can be calculated from the load C-R A=24 kN -9kN =15 kN. For any point between C and B the forcefulness to the right is up and the shearing force is therefore negative every bit was shown before in Fig. 1. Information technology should exist noted that the shearing force changes suddenly at point C. This is shown in Fig. four(a).
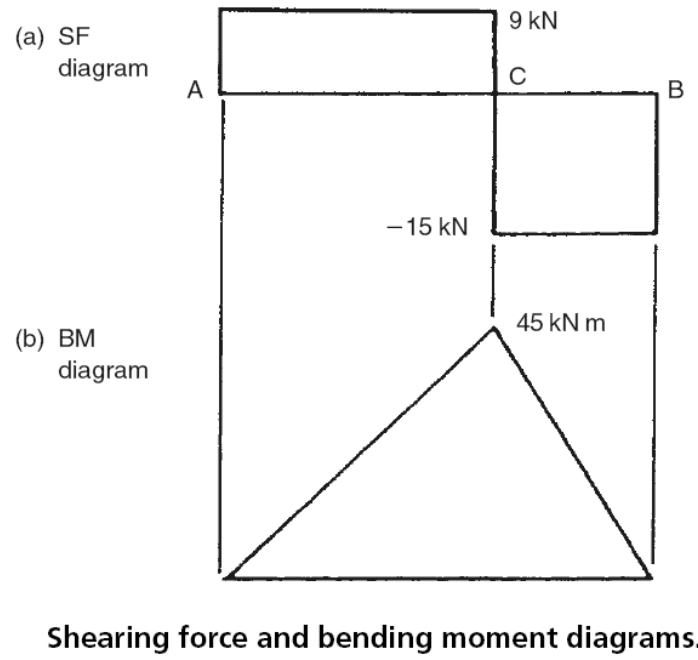
Fig four
The corresponding bending moments are shown in Fig. 4(b). The bending moment at A is zero, since there are no forces to the left of point A. At a point 1 m to the right of signal A the moment of the but force R A to the left of this point is R A ×1m =9 kN chiliad. Every bit this moment most A is clockwise the moment is positive (+nine kN m). At points 2, iii, four and 5 m to the right of A the angle moments are respectively:
R A ×2m =9kN ×2m=18 kNm
R A ×3m =9kN ×3m =27 kNm
R A ×4m =9kN ×4m =36 kNm
R A ×5m =9kN ×5m =45 kNm
Since all these are clockwise moments they are all positive bending moments. For points to the right of C, the load at C as well every bit RA must be considered or, more than simply, as previously demonstrated RB alone can be used. At points 5, 6 and 7 one thousand from A, the bending moments are respectively:
R B ×3m =15 kN ×3m =45 kNm
R B ×2m =15 kN ×2m = 30 kNm
R B ×1m =15 kN ×1m =15 kNm
As these moments to the correct of the points considered are anticlockwise, they are all positive bending moments. At B the bending moment is zero every bit at that place is no strength to its right.
The results are summarized in Tabular array 1
| Tabular array 1 Shearing force and angle moment values for Fig.4 | ||||||||||
| Distance from A(chiliad) | 0 | 1 | 2 | 3 | iv | 5 | half dozen | vii | 8 | |
| Shearing Strength (kN) | +9 | +9 | +9 | +nine | +9 | +9 | -fifteen | -15 | -15 | -fifteen |
| Bending Moment (kNm) | 0 | +nine | +18 | +27 | +36 | +45 | 30 | +15 | +xv | |
Using the results from Tabular array ane the shear force and angle moment diagrams can be drawn as shown in Fig. 5. A stepped shearing forcefulness diagram with simply horizontal and vertical lines can only exist when the axle only carries concentrated, point loads. A sudden alter in shearing forcefulness occurs where the concentrated loads, including the reactions at the supports, occur. For this type of unproblematic loading the bending moment diagram as well consists of direct lines, usually sloping. Sudden changes of bending moment cannot occur except in the unusual circumstances of a moment being practical to a beam as distinct from a load.
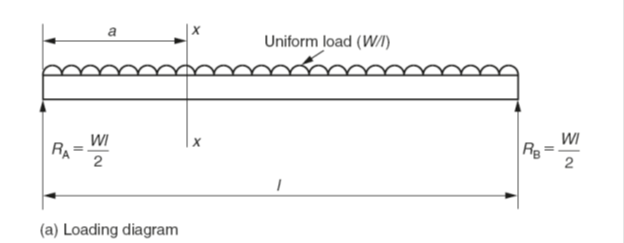
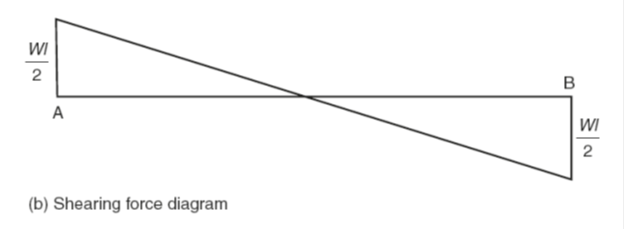
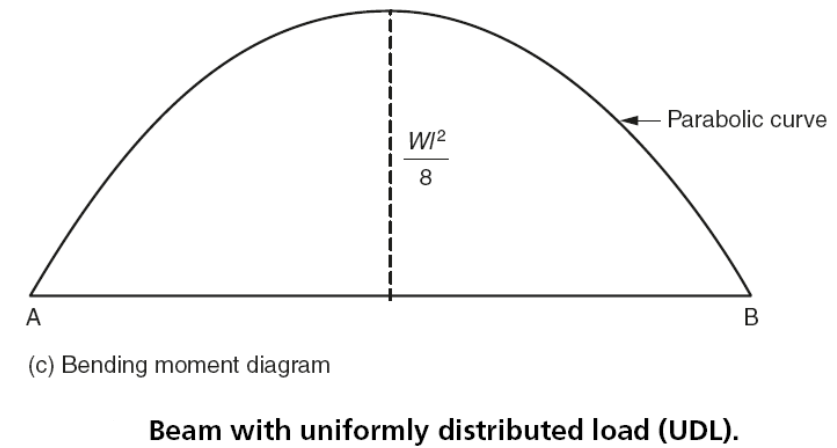
Fig 5
In do a beam loaded with concentrated point loads alone cannot exist. This is considering the beam itself has mass and, therefore, weight. In a axle of compatible cross-section this represents a uniform load throughout the length of the beam. The outcome of compatible loading volition now exist considered.
Figure v(a) shows a uniformly loaded beam of length l and weight W. The but point loads being the reactions at the supports R A and R B. Since the loading is symmetrical R A and R B will both equal Westward/2. The shear force diagram shows maximum values at the points of support and zero shear at the midpoint. This time, withal, the line joining the shearing force is a sloping line passing through the midpoint.
Take a section Xx at a distance a from the left-hand support R A:
The shearing forcefulness at Xx =(Wl/two) -(W× a)
Since this is the equation of a direct line the shear strength diagram is shown in Fig. 5(b). Unlike the previous example, this fourth dimension the bending moment diagram is not made up of straight lines but is a continuous curve with a maximum value at the midpoint.
The bending moment M10 at 20 =[(Wl/2) ×a] – [Due west ×a × (a/2)]
Therefore:
K10=Due west/two(la–a two) (1)
This is the equation of a parabola then, its first derivative will be a maximum when:
d1000x /da = 0
Differentiating equation (i):
d1000ten /da =W/two(l -2a) =0
When:
a =l/2
The maximum angle moment occurs at the heart of the span which is only to be expected with symmetrical loading. Hence substituting a =l/ii in equation (one):
Chiliad max =W/two[(50 2/two) -(fifty ii/4)] = Wl 2 /viii
The angle moment diagram is shown in Fig. 5(c). Apart from the axle shown in Fig. 5(a) where the uniform load resulted from gravity acting on the mass of the axle itself, the only other occasion when a beam is uniformly loaded is when it is carrying a compatible panel of masonry.
More oft, there is a combination of point loads and uniform loading every bit shown in the loading diagram Fig. 6(a).
(a) Summate reactions R A and R C by taking moments nigh A:
(45 ×2) +(12 ×ix) ×4.5 +(24 ×12) =9R C
Thus: R C =96 kN and R A =81 kN
(b) Shearing forces (let x be any distance from A):
For 0 ≤x≤ 2, shear forcefulness =(81 – 12ten) kN
For 2 ≤x≤ ix, shear forcefulness =(81 – 12x – 45) = (36-12x) kN
For 9 ≤x ≤12, shear force= (81-12×9-45+96)=+24 kN
These results are depicted past straight lines as shown in Fig. half dozen(b)

Fig 6
(c) Bending moments (let ten be any altitude from A):
For 0 ≤x ≤2, G =81x-12(x 2/2) =81ten-sixx twokNm
Therefore: at A, x =0 and MA =0
at B, x =ii and G B=162-24=138 kNm
For 2 ≤ten ≤9, M =81x – (12x 2/2) – 45 (10-two)=36ten-sixx 2+90 kNm (ii)
At x =ii M B =72-24+90= 138 kN m (as to a higher place)
At x=9 Thousand C =324-486+90 =-72 kNm
The maximum angle moment occurs between the points B and C where dM/dx= 0.
Note this is the aforementioned betoken that the shearing forcefulness is too zip. From equation (two):
dM/d10 =36-12x=0
Therefore:
x =3m
Substituting ten=iii in equation (2):
(36 ×3)-(6×32)+90=144 kN m.
Thus the maximum bending moment is 144 kN thou and it occurs at a point 3 m from A. Contraflexure will occur when the bending moment is cipher. That is, the positive root of equation (2) when information technology is equated to nix.
36ten-6x ii+90=0
Therefore:
x =7.9m (the only positive solution)
Therefore contraflexure occurs at a betoken 7.9 m from A.
Beams (cantilever)
Likewise as being simply supported as in the previous examples, beams may also exist in the class of a cantilever. That is, only one end of the axle is supported and the remote end from the support is unsupported as shown in Fig. 7(a). The supported finish of the beam may be built into masonry or it may exist a projection from a but supported beam. A typical shearing force diagram and a typical bending moment diagram for a cantilever axle with full-bodied, bespeak loads are shown in Fig. 7(b) and (c).
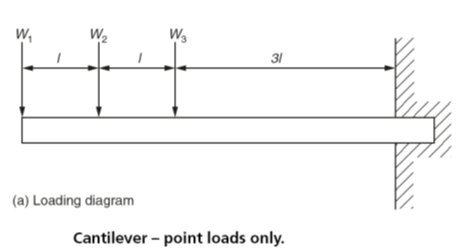
Fig. seven

Fig. viii
Source: https://engineersfield.com/beam-analysis/
0 Response to "what is the resultant moment about a due to the distributed load? (figure 1)"
Post a Comment